[탐색 알고리즘] - DFS 이해하기

코테를 하면서 dfs랑 bfs를 이해하기가 좀 어려웠다.

그래도 머리가 좀 굵어져서인지 최근에는 코테 문제를 풀면서 dfs를 어느 정도 활용할 수 있게 되었다.

오늘 이 시간에는 dfs에 대해 이해하면서 코테 사이트에서 본 문제를 예제 삼아 어떻게 풀었는지에 대해 흐름을 따라가고자 한다. 

1. DFS

1.1 정의

탐색 알고리즘 종류 중의 하나이다. Depth First Search. 줄여서 DFS로 불리며 우리나라 말로는 '깊이 우선 탐색'으로 표기할 수 있다. 말 그대로 탐색 시 깊숙이 들어가서 우선 탐색한다.

깊이 우선 탐색 예시

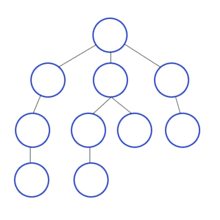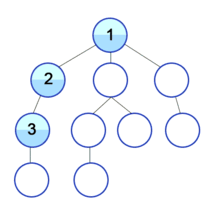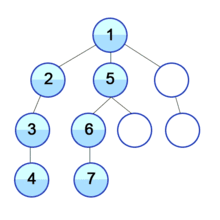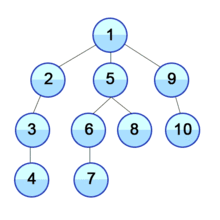
1.2 구현

일반적으로 재귀호출을 사용하여 구현하지만, 단순한 스택 배열로 구현하기도 한다. 

갈림길이 나타날 때마다 '다른 길이 있다'는 정보만 기록하면서 자신이 지나간 길을 지워나간다. 그러다 막다른 곳에 도달하면 직전 갈림길까지 돌아가면서 '이 길은 아님'이라는 표식을 남긴다. 그렇게 갈림길을 순차적으로 탐색해 나가다 목적지를 발견하면 그대로 해답을 내고 종료.

1.3 특징

단순 검색 속도 자체는 BFS에 비해 느리다. 하지만 검색이 아닌 순회를 할 경우는 많이 쓰인다.

1.4 장단점

1.4.1 장점

• 단지 현재 경로상의 노드들만을 기억하면 되므로 저장 공간의 수요가 비교적 적다.
• 목표 노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있다.

1.4.2 단점

• 해가 없는 경로에 깊이 빠질 가능성이 있다. 따라서 실제로는 미리 지정한 임의 깊이까지만 탐색하고 목표 노드를 발견하지 못하면 다음 경로를 따라 탐색하는 방법이 유용할 수 있다.
• 얻어진 해가 최단 경로가 된다는 보장이 없다. 이는 목표에 이르는 경로가 다수인 문제에 대해 깊이 우선 탐색은 해에 다다르면 탐색을 끝내버리므로, 이때 얻어진 해는 최적이 아닐 수 있다는 의미이다.

2. 문제로 보는 DFS 사용

2.1 백준 1260번 문제

https://www.acmicpc.net/problem/1260

1260번: DFS와 BFS

*bfs 는 풀지 않았고, dfs만 예제를 이용했다.

2.1.1 사고의 흐름

1. 정점과 간선의 관계를 dictionary 형태로 만들었다.

N, M, V = [int(x) for x in input().split(" ")]
args = [list(map(int, input().split(" "))) for _ in range(M)]  # 간선이 연결하는 두 정점의 번호를 리스트로 만듦


def nodes_append(k: int, v: int, nodes: dict):
    nodes.setdefault(k, deque()).append(v)
    nodes[k] = deque(sorted(nodes[k]))  # 정점 번호가 작은 것을 먼저 방문해야한다.


nodes = {}
# nodes에 정점과 간선의 관계를 dictionary 형태로 채워넣음
for k, v in args:
    if v not in nodes.get(k, []):
        nodes_append(k, v, nodes)

    if k not in nodes.get(v, []):
        nodes_append(v, k, nodes)

 

이때 문제 요구사항에 정점 번호가 작은 것을 먼저 방문해야 하므로 정렬을 한다.

 

2. 노드를 생성했으면 dfs 함수를 통해 노드 순회한 순서를 결괏값에 넣는다.

def dfs(v):
    nonlocal result
    if v not in nodes:  # 연결된 정점이 없다면 return
        return

    if v not in result:  # 결과 값에 없다면 v 를 추가(첫 정점을 추가 하기 위한 코드)
        result.append(v)

    while nodes[v]:
        node = nodes[v].popleft()  # 순서대로 꺼내기 위해서
        if node not in result:
            result.append(node)
            dfs(node)
        else:
            continue
                
                
dfs(V)

3. 전체 코드이다.

# https://www.acmicpc.net/problem/1260
from collections import deque

N, M, V = [int(x) for x in input().split(" ")]

args = [list(map(int, input().split(" "))) for _ in range(M)]
print(args)


def nodes_append(k: int, v: int, nodes: dict):
    nodes.setdefault(k, deque()).append(v)
    nodes[k] = deque(sorted(nodes[k]))  # 정점 번호가 작은 것을 먼저 방문해야한다.


def solution():
    nodes = {}
    result = []

    for k, v in args:
        # 양방향이므로 nodes 서로서로 추가.
        if v not in nodes.get(k, []):
            nodes_append(k, v, nodes)

        if k not in nodes.get(v, []):
            nodes_append(v, k, nodes)

    def dfs(v):
        nonlocal result
        if v not in nodes:  # 연결된 정점이 없다면 return
            return

        if v not in result:  # 결과 값에 없다면 v 를 추가(첫 정점을 추가 하기 위한 코드)
            result.append(v)

        while nodes[v]:
            node = nodes[v].popleft()  # 순서대로 꺼내기 위해서
            if node not in result:
                result.append(node)
                dfs(node)
            else:
                continue

    dfs(V)

2.2 프로그래머스 타겟 문제

https://school.programmers.co.kr/learn/courses/30/lessons/43165

프로그래머스

2.2.1 사고의 흐름

계산을 위한 노드는 이미 만들어져 있다. numbers가 있으므로 이를 순회하면서 이전 결과 값을 더하거나 빼거나의 경우의 수를 계산 한 뒤 마지막 깊이(여기서는 numbers의 길이가 되겠다.)까지 왔을 경우 결괏값과 target 이 같으면 result를 더하면 된다고 생각했다.

# 프로그래머스 dfs 문제 - 타겟 넘버

def solution(numbers: list, target):
    answer = 0
    length = len(numbers)

    def dfs(idx, number, result):
        nonlocal answer
        result += number
        if result == target and idx == length - 1:
            answer += 1
            return

        next_ = idx + 1
        if next_ == length:
            return

        dfs(next_, numbers[next_], result)
        dfs(next_, -1 * numbers[next_], result)

    dfs(0, 1 * numbers[0], 0)
    dfs(0, -1 * numbers[0], 0)

    return answer

---

참고

1. https://namu.wiki/w/%EA%B9%8A%EC%9D%B4%20%EC%9A%B0%EC%84%A0%20%ED%83%90%EC%83%89

깊이 우선 탐색 - 나무위키